TCG提出的可信平台体系结构,它的核心是一个防篡改的安全硬件设备,称为TPM[11](Trusted Platform Module,可信平台模块)。作为内嵌到计算平台中的信任根,它可以看作一个微型计算机,具备四个主要功能:对称/非对称加密、安全存储、完整性度量和签名认证。完整性度量和存储功能依靠TPM内部的PCR(Platform Measurement Log,平台配置寄存器)来实现,PCR至少16个,每个PCR的大小是20字节,用来存储大量平台测试结果的摘要,计算公式为:
PCR[n] = SHA-1(PCR[n] || measured data)
这里n代表更新的PCR的编号。与完整性度量相关的另一个结构是SML(Stored Measurement Log,度量存储日志),用于记录PCR的更新事件序列。PCR和SML有着密切的关系,没有PCR中摘要的消息,SML中保存的事件记录便会变得毫无意义(没有办法阻止生成错误的事件记录);同样,没有SML内的内容,仅仅得到PCR中摘要的值也毫无用处(PCR摘要的上下文信息将会丢失)。PCR提供平台是否被入侵的证据,这是因为SML中存储着PCR值的变更记录,经过一定的哈希计算,就能得到当前平台的完整性度量值,将计算得到的摘要值与当前PCR中的摘要值比较,就可判定当前的平台是否被篡改。
2.2.2平台认证
完整性报告是用来证明完整性存储的过程,依靠可信平台的鉴定能力证明保护区域中完整性度量值存储的正确性。当一个校验者希望验证远程平台配置的正确性时,它将请求特定的 值和与之对应的SML记录。计算的散列值保存在PCR里面,而SML保存着被度量值的序列,每个序列公用一个通用摘要。这些被度量值附加在通用摘要后再次散列,通常称为摘要的扩展,扩展保证操作的顺序。校验者利用SML记录进行摘要扩展得到摘要值,通过与PCR中的摘要值比较,即可判断存储的完整性。
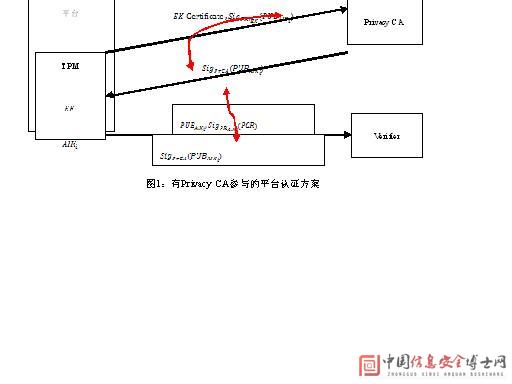
PCR值的有效性通过TPM在其上进行签名得以保证。每个TPM由EK(Endorsement Key,签注密钥)唯一标识,它是一个RSA密钥对。如果直接采用EK私钥对PCR进行签名,这时必须公开EK公钥,从而泄露平台的身份。为了保护平台的隐私,从安全的角度考虑,我们要尽量少用EK,因此不能直接用它对PCR值进行签名。为了解决这个问题,TCG在TPM Specification 1.1中提出了 参与的平台认证方案,它不直接用EK对PCR值进行签名,而是用EK证书申请AIK(Attestation Identity Key,身份证明密钥,RSA密钥对),然后利用AIK的私钥对PCR值签名。理论上,同一个EK可以申请无穷多个AIK,针对不同的校验者使用不同的AIK,在一定程度上保护了平台的隐私。
尽管如此,有Privacy CA参与的平台认证仍然存在较大的缺陷,如图1所示,主要体现在以下三点:
(1)每次需要使用AIK时,平台都需要通过EK证书与Privacy CA交互,这就要求Privacy CA具有高响应
能力,其应用易导致可信平台验证的瓶颈。
(2)只要Privacy CA与校验者联合,AIK证书将与EK证书关联,校验者将能唯一确认平台的身份;而假如平台与Privacy CA联合,就可以欺骗校验者。
(3)现实的商业模型中,Privacy CA并不存在。用户需要信任Privacy CA不与校验者联合,故Privacy CA不能由服务提供方(校验者)担当;而校验者需要相信Privacy CA仅给TPM为有效的平台颁发AIK证书,于是Privacy CA不能由用户担任。
考虑到这点,TCG在TPM Specification 1.2中又提出了DAA[7](Direct Anonymous Attestation,直接匿名认证)协议,旨在解决可信平台的认证和隐私保护问题。与有Privacy CA参与的平台认证方案相比,DAA主要有两方面的优势:(1)DAA Issuer与平台完成Join协议后,平台就获得一个DAA证书,以后每次验证都不再需要DAA Issuer的参与,这样就解决了Privacy CA的响应瓶颈问题;(2)平台只是采用零知识证明协议[12]证明它拥有一个合法的DAA证书,而不需要泄露DAA证书的内容,这样即使DAA Issuer与校验者联合,也不能确定平台的身份,具有更好的匿名性。
3. 构建基于可信计算的P2P信任模型
3.1 基本概念
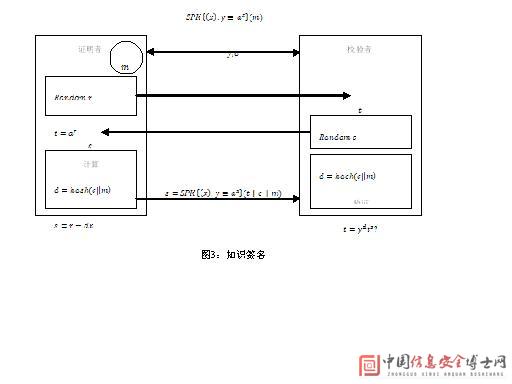
定义1(盲签名[12]):盲签名允许一个实体获得消息的签名而签名者并不知道消息的内容,包括对消息进行盲化和对签名去盲化两个过程,用数学公式表示为 。
定义2(零知识证明[13]):零知识证明允许证明者在不泄露任何秘密的情况下,向校验者证明他知道该秘密。
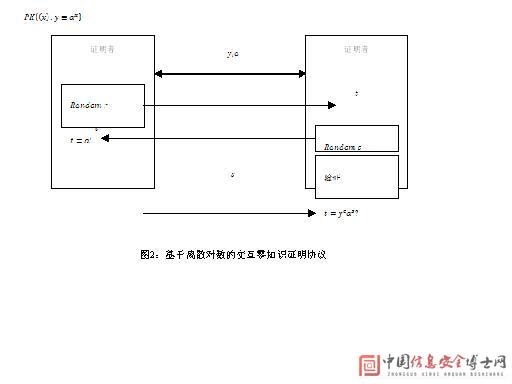
本文主要涉及基于离散对数的零知识证明,为了描述这些协议,我们采用Camenisch和Scadler引进的符号表示[14]。我们将y≡axmodT简记为y≡ax ,而符号PK{(x):y≡ax}表示知识“x是整数且满足y≡ax ”的零知识证明,其中x是秘密而y和a公开。图2所示的是一个典型的PK{(x):y≡ax}协议,容易看出,恢复出s值的难度等价于解t≡ar的离散对数。
(责任编辑:adminadmin2008)