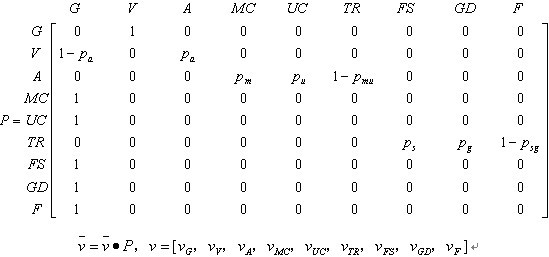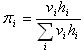状态转移模型最大的优点在于，解决了入侵容忍系统因为复杂的结构而难以对各种安全问题进行归类和定义的难点，把系统状态抽象地划分为9种状态，具备了良好的通用性，可以适应各种不同的入侵容忍策略和架构，也能够应对不同类型的攻击行为，因此成为后来很多研究的基础模型。但是，状态转移模型的一个引申出的难题在于：在实际分析中，如何判定系统处于何种状态。

3.2 基于状态转移模型的SMP模型
    Bharat B.Madan等^[4]人在之前的研究基础上进一步考虑了漏洞存在时间与状态转移概率之间的关系，提出用一个基于状态转移矩阵的半马尔可夫模型(SMP模型, Semi-Markov Model)，将时间作为一个参数变量引入安全分析，并提出以平均安全故障时间MTTSF来作为评价系统安全性的指标。通过分析比较各参考文献可以认为，这篇论文是近几年在入侵容忍系统的安全性分析方面最重要的研究成果之一。
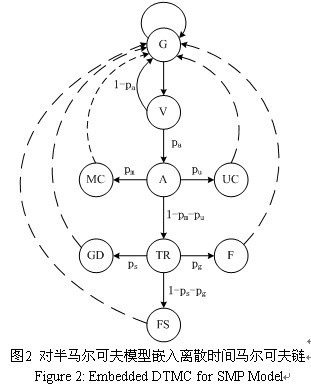
    该模型将系统的状态变化参数化为两大类参数：平均持续时间h和状态转移概率p。另外，状态转移模型并不便于量化分析，所以这里对状态转移模型嵌入离散时间马尔可夫链(DTMC)，各个状态之间的转移概率以不同的变量参数表示，如图2。在SMP模型中设定的主要参数如下：
hi，i∈(G，V，A，UC，MC，TR，FS，GD，F)，hi表示系统在i状态所滞留的平均时间；
pa 成功地利用漏洞发动一次攻击，使系统由V状态进入A状态的概率；
pu 攻击行为成功，并未能被系统检测出的概率；
pm 系统成功屏蔽攻击行为的概率；
pg 系统通过降级服务抵抗攻击的概率；
ps 系统对攻击采取安全停止措施的概率。

假设每个状态出现的概率为vi，则  ；
各状态之间的转移概率可以用以下矩阵表示：

 由以上公式可以得出vG以及各个状态出现概率：

 最后，每个状态的稳态概率通过公式算出：

将其中表示安全状况受损的，必须靠人工手段进行恢复的状态定为吸收状态(Absorbing States)Xa={UC，FS，GD，F}。其余状态定为瞬时状态

(责任编辑：adminadmin2008)