2 图像复制伪造区域检测算法
2.1 算法思想
图像块的DCT量化系数和PCA特征值所使用的方法理论基础:图像能量主要集中在前面的几个大系数上,因此通过忽略一些小的变换系数值来达到减少数据量的目的。但是他们的算法都是直接以原始图像为根本特征提取的原数据,然后进行特征值降维提取。但图像较大时,因其一次移动一个像素的滑窗操作使得图像块的数目非常大。
本文首先采用离散小波变换DWT(Discrete Wavelet Transform)来缩小图像的尺寸。小波变换是一种时域-频域(或空域-频域)变换,同时具有时(空)域和频域的良好局部化性质。图像经过小波多分辨率分解之后,所得到的低频部分仍然保持原图像的概貌和空间特性。经过DWT变换,低频图像尺寸就减少到近似原始图像的
向量的选取是整个检测算法的关键,各图像块的特征能否很好的表征各图像块,直接关系到检测的效果。基于不变矩(moment invariants)检测copy-move型图像篡改在文献【模糊不变矩】中首次提出。已经证明不变矩作为特征是一种有效的图像分析和识别的方法,其结果对旋转、平移和缩放等几何图像篡改具有很好的检测效果。本文选取文献[3]提出的7个不变矩作为个重叠块的特征向量,图像f(x ,y )的p+q阶矩定义为:
相映f(x,y)的p+q阶中心矩
其中
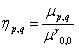
其中
+
矩特征的定义和计算公式建立在对一个区域内部灰度值或者是边界灰度值分析基础上的,是一个全局量的描述,描述了对象的整体特征。文献[3已经详细证明它们对平移、旋转、镜像以及缩放等几何操作具有很好的不变性。由此,可对图像各重叠块提取以上7个特征值,组成7维特征向量为:
其中mn为图像行和列的总数,a,b为滑动窗口的行和列的大小。(i,j)为图像各重叠块左上角像素坐标。很明显,经过提取图像块的不变矩特征,使得原小波低频系数块的特征空间由a X b下降到7维。
像相似性匹配检测中,相似性度量包括两类:差值测度和相关测度。相关测度则采用图像所对应矢量的夹角余弦,而差值测度采用图像所对应矢量之差的范数。在此我们采用了欧氏距离的相似性[5]度量方法。模式样本量Bi,j 与Bi+k,j+g 之间的欧氏距离定义为:
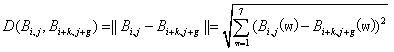 …………………(7)
…………………(7) 其中w为特征空间的维数。若一个图像块是另一个图像块的复制块,则两个图像块欧氏距离
2.2 算法步骤
提出一种能有效检测和定位图像copy-move篡改的检测算法,算法的流程如图1所示。首先对检测图像进行小波变换,然后对小波低频分量进行固定大小的逐像素滑窗操作,对每个图像块进行不变矩提取作为图像块的特征Bi,j ,再对各Bi,j 特征向量之间进行欧氏距离计算,选定阈值判别各块之间的相似性,最后统计各项是块之间的偏移频率,定位复制伪造区域。
(责任编辑:adminadmin2008)





