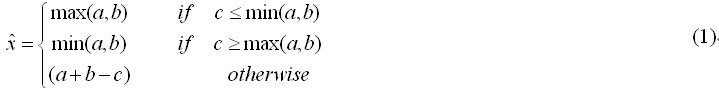假定图像的大小为
，当前的载体灰度像素值为
，其对应得预测图像像素值为
，则预测误差图像像素值为
。 的邻近像素灰度值定义为a，b，c，如图2(a)所示，当 位于图像的最后一行和最后一列的特殊位置时，即(M,j) (j=1,…,N-1), (i,N)(i=1,…,M-1),(M,N)，相对应的a，b，c如图2(b)(c)(d)所示。预测算法表达式[14]见公式(1)：
2.2 特征函数统计矩
随机过程的统计样本可完全由联合概率分布描述：一连续取值的随机过程由概率密度函数(PDF)描述，一离散取值的随机过程由概率质量函数(PMF)描述。由于随机变量的分布律和特征函数之间存在一一对应的关系，随机变量的分布函数由其特征函数唯一确定，并且特征函数具有良好的分析性质。矩是随机变量最广泛的数字特征，是一种非常重要的特征量。
特征函数g(t)的k阶统计矩和k阶绝对统计矩定义分别见公式(2) (3)：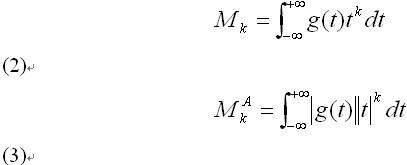 
由
经
加权生成，
拖尾的任何变化，即对应PDF的高频成分在
中都将被放大。CF的统计矩Mk（或绝对统计矩）与p(x)的k阶导数在x=0处的值相关： 
如果CFg(t)有长的拖尾，则较大，对应的PDFp(x)为尖峰。
若独立同分布序列(i.i.d.)
，其PDF未知，则可选择其经验CF矩做统计分析。为此，对
进行PDF估计，估计值可采用直方图 ，直方图可视
为概率密度函数p(x)的离散形式，其中M为直方图水平轴变量的个数，令
。
L点离散CF定义见公式(7)：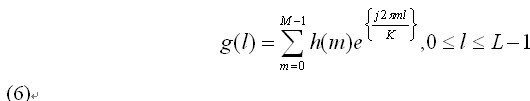 
Wang[ 11]定义离散特征函数k阶绝对矩如公式(8)：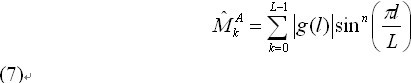 
把图像的灰度值或变换域系数看成随机变量，其分布反映在图像统计特征上即为像素或系数直方图PMF，记为h(x)，h(m)为直方图h(x)估计的概率密度函数的离散形式。
2.3 特征提取
隐写分析中一般采用概率密度函数矩（或概率质量函数经验矩）或特征函数矩特征。本文选择小波系数直方图为PMF作为PDF的离散估计，在此基础上定义特征函数，并采用公式(7)中经验CF统计矩为特征。图像首先通过3级Haar小波变换获得9个细节子带：水平子带Hi，垂直子带Vi和对角子带Di，i=1，2，3；以及3个近似子带Li，i=1，2，3。对第一级对角子带D1做再一级小波分解以提高学习系统的性能[13]，由此获得4个子带：
。对D1做进一步分解的原因是因为D1是Haar小波变换中最精细的细节子带，其每个系数包含了一个4像素块的对角差分，D1的再次小波分解系数包含了更多的邻域像素，因此
能揭示更多的相邻像素间的差异信息，计算 的CF矩构成训练集的一部分。图像的有效特征为上述17个子带的前3阶CF矩51维；对预测误差图像得到同样的51维特征，由此得到总共102维特征向量。
3. 主成分分析法选择特征
并不是特征越多，分类性能越好，过多地特征有时反而会影响分类性能，因此选择使用主成份分析法(PCA) [12] 进行特征降维。采用基于离散K-L变换的PCA。若N个模式样本
是有类别标签
的样本集，各类的先验概率是Pi，母体均值向量是
，总体均值向量
，则可得2类情况下总的类内、类间离散度矩阵。
(责任编辑：adminadmin2008)
